Imagina un tiempo en el que las personas no se preguntaban ¿Qué es Álgebra?, porque no podían representar incógnitas con letras o símbolos, y donde los cálculos eran puramente numéricos. Así era el mundo antes de que el álgebra se convirtiera en una herramienta matemática fundamental. Este concepto no solo cambió la forma en que entendemos los números, sino que permitió avances en áreas tan diversas como la ingeniería, la economía y la informática.
¿Qué es Álgebra?
Es una rama de las matemáticas que se ocupa de estudiar las relaciones entre números y símbolos, utilizando letras para representar valores desconocidos o variables. A diferencia de la aritmética, que trabaja solo con números conocidos,
El álgebra introduce incógnitas que pueden tomar diferentes valores dependiendo del contexto.
Las primeras formas de este concepto se desarrollaron en la antigua Babilonia, donde se resolvían ecuaciones cuadráticas de manera geométrica. Sin embargo, fue en el mundo árabe, alrededor del siglo IX, donde el álgebra se formalizó como una disciplina independiente, gracias a los trabajos de Al-Juarismi, matemático y astrónomo persa.
El término “álgebra” proviene del título del libro de Al-Juarismi, “Kitab al-Jabr wal-Muqabala”, que significa “El compendio del cálculo por reintegración y comparación”. Este tratado sentó las bases del álgebra moderna, proporcionando soluciones sistemáticas a ecuaciones lineales y cuadráticas mediante operaciones simbólicas.

¿Para qué nos sirve?
El álgebra es mucho más que una herramienta para resolver ecuaciones. Su utilidad abarca una vasta gama de aplicaciones en la vida cotidiana, desde cálculos financieros hasta la toma de decisiones lógicas. En el ámbito académico, es fundamental para el desarrollo del pensamiento abstracto y la resolución de problemas complejos. Ayuda a los estudiantes a desarrollar una capacidad analítica, permitiendo expresar relaciones matemáticas y resolver problemas con incógnitas.
En el día a día, utilizamos el álgebra sin darnos cuenta. Por ejemplo, cuando calculamos cuántas horas nos quedan para cumplir con una tarea o cuándo ajustar un presupuesto familiar. Además, en campos como la ingeniería, la economía y la física, el álgebra permite modelar situaciones reales mediante ecuaciones matemáticas que representan relaciones entre diferentes variables.
Operaciones en Álgebra.
Las operaciones algebraicas consisten en manipular expresiones que contienen números y variables. Las operaciones más comunes incluyen la suma, resta, multiplicación y división de términos algebraicos. Una expresión algebraica puede contener una o varias variables, y el objetivo de la operación es “despejar” esas variables, es decir, resolverlas.
Existen varios tipos de expresiones algebraicas:
- Monomios: Son expresiones que contienen un solo término ( por ejemplo, 5x5x ).
- Binomios: Expresiones que contienen dos términos ( por ejemplo, 3x+43x+4 ).
- Polinomios: Expresiones con tres o más términos ( por ejemplo, 2×2+3x+42×2+3x+4 ).
Para resolver ecuaciones algebraicas, se utilizan diversas técnicas, desde la simplificación de expresiones hasta la factorización. Un ejemplo clásico de operación algebraica es la resolución de ecuaciones cuadráticas, que tiene aplicaciones en la física y la ingeniería para modelar fenómenos naturales como el movimiento de objetos.
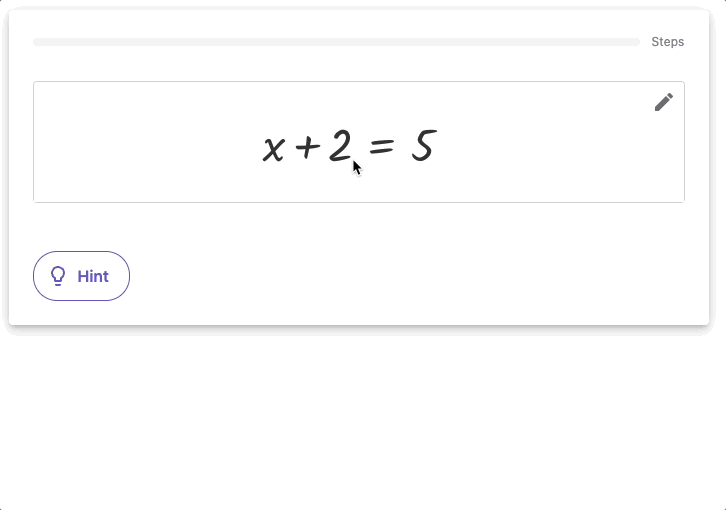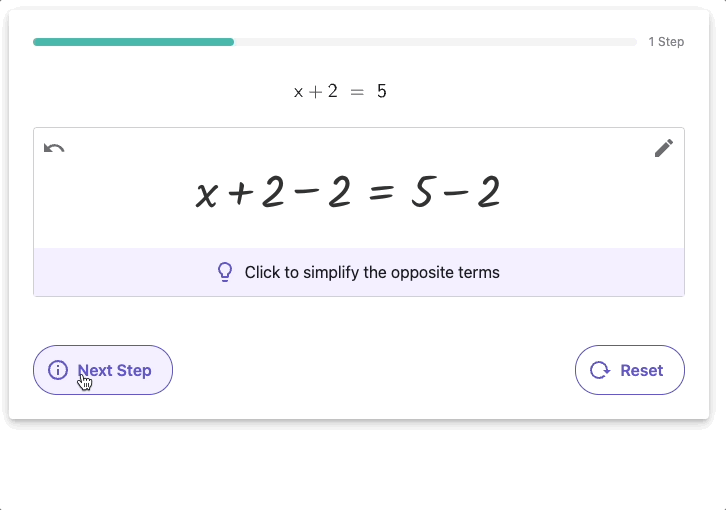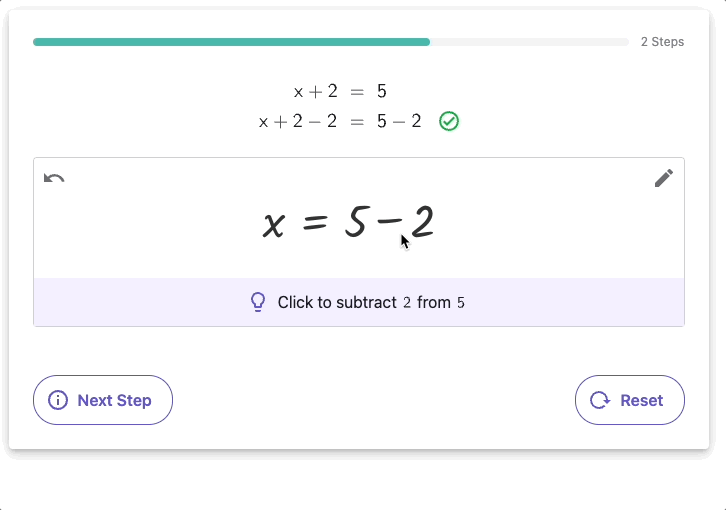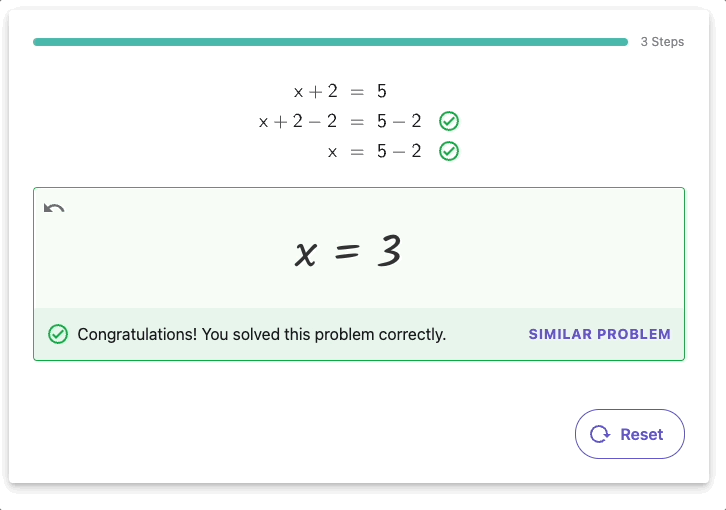
Aplicaciones modernas de Álgebra.
El álgebra ha trascendido las matemáticas puras y se ha convertido en una herramienta esencial en diversas disciplinas científicas y tecnológicas. A continuación, se detallan algunas de sus aplicaciones más relevantes:
Ingeniería: En la ingeniería civil y mecánica, es fundamental para el diseño de estructuras, cálculos de resistencia y la creación de modelos físicos. Los ingenieros usan ecuaciones algebraicas para determinar la cantidad exacta de materiales necesarios o para predecir el comportamiento de una construcción bajo diferentes condiciones.
Informática: El álgebra booleana, una rama que trabaja con valores binarios (0 y 1), es la base de la programación y la computación. Se utiliza para el diseño de circuitos lógicos y la creación de algoritmos que permiten el funcionamiento de dispositivos electrónicos, como ordenadores y teléfonos móviles.
Economía: En economía y finanzas, se utiliza para modelar escenarios de negocio, calcular el crecimiento económico y realizar predicciones basadas en datos pasados. Las ecuaciones algebraicas permiten optimizar recursos y analizar el impacto de variables como la inflación o los tipos de interés en la economía global.
Conclusión.
El álgebra no solo es una herramienta matemática, sino una manera de pensar que ha cambiado el curso de la historia humana. Desde sus inicios en Babilonia y su formalización en el mundo árabe, hasta sus aplicaciones modernas en ingeniería y computación, ha demostrado ser una disciplina fundamental para el avance del conocimiento. Al estudiar álgebra, no solo aprendemos a resolver ecuaciones, sino a enfrentarnos a los desafíos del mundo real con un enfoque lógico y sistemático.
El álgebra sigue siendo una de las áreas más importantes de las matemáticas, y su estudio nos prepara para enfrentar los desafíos del futuro, en campos tan diversos como la tecnología, la ciencia y las finanzas.
Referencias:
Dimex. (2024). ¿Qué es la educación STEM?. Recuperado de https://dimexideas.com/que-es-la-educacion-stem/
Historia de las matemáticas: Referencias sobre la evolución de las matemáticas y su impacto en la sociedad. Katz, V. J. (2009). A history of mathematics: An introduction. Pearson.
Contribuciones científicas del mundo islámico: Descripción del avance científico y matemático en la época islámica. Saliba, G. (2007). Islamic science and the making of the European Renaissance. MIT Press.
Contribuciones de René Descartes y la geometría analítica: Cómo las contribuciones de Descartes ayudaron a la evolución de las matemáticas. Garber, D. (2001). Descartes embodied: Reading Cartesian philosophy through Cartesian science. Cambridge University Press.
Influencia de la matemática en la ingeniería moderna: Cómo las herramientas matemáticas ayudan en campos como la ingeniería civil y mecánica. Goodchild, M. F., & Janelle, D. G. (2004). Spatially integrated social science. Oxford University Press.




